Virality occurs when your product spreads from customer to customer. This is often the cheapest way to acquire new customers. Apps usually provide mechanisms to help users invite friends or offer referral programs as incentives. Achieving success requires extensive experimentation and the use of right metrics for accurate analysis.
Virality is typically measured and modelled with two key metrics: Viral Coefficient and Viral Cycle Time. These metrics are great for theoretical models but difficult to measure and work with in practice. To address this, I use Viral Cohort Analysis. This helps uncover the nature of a product’s virality, allowing me to determine workable values for the Viral Coefficient and Viral Cycle Time.
First, let’s examine the two traditional metrics used to model virality:
Viral Coefficient measures how many new customers each existing customer invites to the platform. A viral coefficient above 1 means exponential growth, as each customer brings in more than one new customer, rapidly expanding the customer base.
Viral Cycle Time is the average time from a new customer’s signup to when their invitees sign up. This process involves several steps: the customer learns to use the app, realizes its value, and then starts inviting others.
Optimizing these two metrics can dramatically accelerate your business growth!
For instance, imagine beginning with 1,000 customers. If your viral coefficient is 2 and the viral cycle time is 2 months, you would reach 63,000 customers in 10 months. However, increasing the viral coefficient to 4 could skyrocket your customer base to 1,365,000 in the same period.
Alternatively, reducing the cycle time to 1 month while keeping the viral coefficient at 2 could increase your numbers to 2,047,000 customers in 10 months. These three growth scenarios are illustrated in Figure 1

This highlights the incredible potential of virality and the importance of short viral cycle times. It’s crucial to encourage users to invite their friends as early as possible.
It’s worth mentioning that, in reality, achieving and maintaining a viral coefficient above 1 is rare and often unsustainable over long periods. For most apps, referral mechanisms are primarily a way to reduce Customer Acquisition Cost (CAC) slightly.
What’s the problem with these two metrics?
When using these two metrics in simulations, a user waits the Viral Cycle Time and then invites the Viral Coefficient’s number of users all at once. After that, they stop inviting anyone. This isn’t how it works in the real world.
Users usually spread out their invitations over an extended period, rather than sending them all at once. An approach to address this is setting specific timeframes for measurement. For example, you can consider only the users invited within the first 90 days after signup. While this approach isn’t perfect, it helps in standardizing measurements and yields more meaningful comparisons, especially during A/B testing.
You might wonder where to set the cutoff for measurements? 30 days, 90 days, or more? It’s hard to enforce such limits without understanding how virality works in your app. This is where Viral Cohort Analysis comes into play.
Welcome to the world of Viral Cohort Analysis:
I haven’t found the term “Viral Cohort Analysis” or “Referral Cohort Analysis” used anywhere yet, and I wonder if this concept has another name. I’m sure this type of analysis has been done before because it’s very useful.
If you’re not familiar with cohort analysis, check out my earlier post. Viral cohort analysis is simply a cohort analysis of how users invite new users.
You divide customers or users into cohorts based on the week (or month) they signed up. Then for each cohort you track how many new customers that cohort invited. See table 1.
Table 1: Each row represents a cohort of users who signed up during the week in the first column. The second column is the number of users in the cohort. The columns w1-w10 represent the 10 weeks following signup, indicating the number of users the cohort invited during each corresponding week.
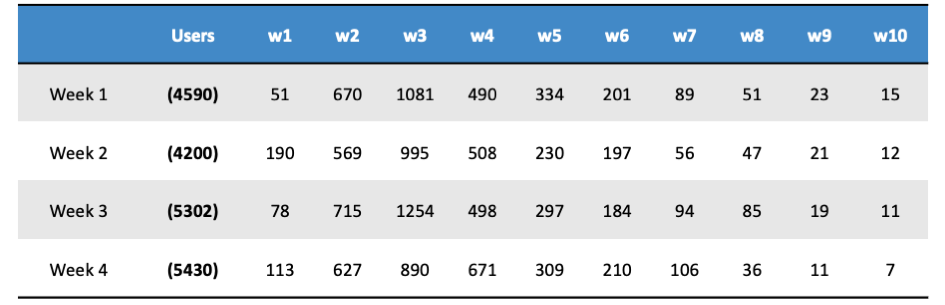
Next, normalize the numbers by dividing them by the number of customers in the corresponding cohort, as shown in Table 2. This makes the numbers comparable between cohorts and the values represent weekly Viral Coefficients. This helps you better understand how virality behaves in your app.
Table 2: This table shows the normalized results from Table 1. The number of new users invited is divided by the total users in the cohort. This makes the numbers more meaningful. For example, a user from the Week 1 cohort will invite 0.01 new users during the first week, 0.15 during the second week, and so on.

You can sum these numbers to get a viral coefficient for any period of your choice. For example, take the cohort of users who signed up during Week 1 and sum the viral coefficients for W1-W4 to get 0.50. Doing this for the other cohorts, you get 0.54 for Week 2 cohort, 0.48 for Week 3 cohort, and 0.42 for Week 4 cohort. The average of these would be 0.49.
With this approach we got a viral coefficient of 0.49 and a viral cycle time of 4 weeks to use in your simulations. This is the lower bound for growth, since in reality the growth is much higher. This is because many of the invites happen before the week 4 and some additional invites will still happen after week 4.
I chose the 4-week timeframe because most invites happen within the first 4 weeks for the app in my example. Week 6 would also be a reasonable cutoff point.
For more accuracy, you could model the invites for each week after signup in your simulations. This way, each user invites the corresponding number of new users each week, resulting in a more precise growth projection. However, in my experience, this is rarely necessary, as no simulation can predict the future accurately. The world changes, your app changes, and users change.
One could argue that a cohort will keep inviting new users indefinitely, resulting in a distribution with a long tail. You could create a probability distribution for invites and use that in your simulations. However, I don’t think it’s necessary for the reasons mentioned above. Additionally, the tail won’t significantly impact growth since the cycle time for those invites is very long.
Where viral cohort analysis is most useful:
I find Viral Cohort Analysis most useful when A/B testing changes to invite mechanisms. These tests might include prompting users for referrals earlier and more often or experimenting with different incentives.
Yu-kai Chou, in his book Actionable Gamification, emphasizes asking users to invite friends only after they reach the “first major win state” and understand the value of your service. Conversely, others like Andrew Chen recommend asking for referrals frequently, even immediately after onboarding.
This is likely not a black-and-white issue and varies between apps. It’s crucial to A/B test to find out what works, and Viral Cohort Analysis helps understand the impact of changes. You can quickly see if invites happen earlier and whether the total invites decrease. In some cases, this might be a favorable tradeoff, as illustrated in Figure 1.
It’s important to note that spamming users with too many popups and messages to refer friends can have negative effects. Therefore, it’s vital to monitor other metrics, such as churn and user activity.
In summary, I hope you now feel better equipped to measure and work with traditional virality metrics—viral coefficient and viral cycle time—and determine them using Viral Cohort Analysis. Additionally, when you experiment with virality features in your app, you should be able to A/B test and use Viral Cohort Analysis to determine the true impact.
I will explore more in future posts how product analytics can can help improve your product and increase revenue. Meanwhile, let me know if you need any help setting up your analytics or if you have other questions related to this topic.
